아르키메데스의 원리

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 역사적 배경
- 2.1. 아르키메데스와 히에론 2세의 왕관
- 2.2. 유레카 일화의 진실성 (보수적 관점에서의 비판)
3. 아르키메데스 원리의 공식과 설명
4. 힘과 평형
5. 부력의 활용
6. 한계점 (Refinements)
참조

1. 개요

아르키메데스의 원리는 물체에 작용하는 부력에 대한 물리 법칙으로, 유체 속에 잠긴 물체는 물체가 밀어낸 유체의 무게와 크기가 같은 부력을 받는다는 것을 설명한다. 이 원리는 시라쿠사의 참주 히에론 2세가 금세공인에게 의뢰한 왕관의 진위를 아르키메데스가 밝혀내는 과정에서 발견되었다는 일화로 유명하다. 아르키메데스는 부력의 크기를 계산하는 공식을 제시했으며, 이 원리는 선박 설계, 잠수함 및 비행선의 부력 활용, 그리고 유레카 캔과 같은 다양한 분야에 적용된다. 하지만 표면 장력이나 복잡 유체와 같은 특정 상황에서는 아르키메데스의 원리가 정확하게 적용되지 않을 수 있다.

2. 역사적 배경

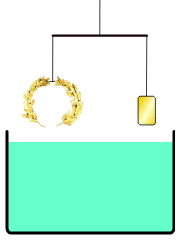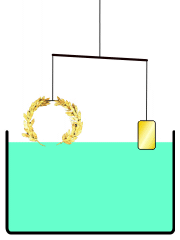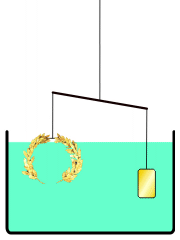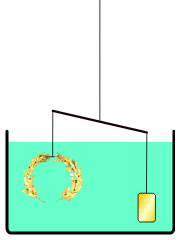
아르키메데스의 원리가 어떻게 발견되었는지에 대한 일화가 전해진다.

히에론 2세는 금세공인에게 순금 왕관 제작을 맡겼으나, 금세공인이 금을 빼돌렸다는 소문이 돌았다. 히에론 2세는 아르키메데스에게 왕관을 훼손하지 않고 진위 여부를 판별할 방법을 찾도록 명령했다. 아르키메데스는 목욕을 하다가 물이 넘치는 것을 보고 부력의 원리를 깨달았다고 한다.

아르키메데스는 욕조에서 뛰쳐나오면서 "유레카(ΕΥΡΗΚΑ|Eureka^el, 알았다!)"라고 외쳤다고 한다.^[15]

이후 아르키메데스는 왕관과 같은 무게의 금괴를 저울에 매달아 균형을 확인하고, 물속에 넣어 밀도 차이를 통해 금세공인의 부정을 밝혀냈다.^[16] 금세공인은 사형에 처해졌다고 전해진다.

아르키메데스와 그 후 학자들은 이 법칙을 자연 과학적인 법칙이 아닌 수학적 원리로 생각했다.

2. 1. 아르키메데스와 히에론 2세의 왕관

히에론 2세는 금세공인에게 순금 왕관 제작을 맡겼으나, 금세공인이 금의 일부를 빼돌리고 다른 금속을 섞었다는 의혹을 제기했다. 히에론 2세는 아르키메데스에게 왕관을 손상시키지 않고 진위 여부를 판별할 방법을 찾도록 명령했다. 아르키메데스는 어느 날 목욕을 하다가 물이 욕조 밖으로 넘치는 것을 보고 부력의 원리를 깨달았다고 한다.^[15]

욕실에서 뛰쳐나온 아르키메데스는 "유레카(ΕΥΡΗΚΑ|Eureka^el, 알았다!)"라고 외치며 알몸으로 뛰쳐나갔다고 전해진다.^[15]

아르키메데스는 왕관과 같은 질량의 금괴를 준비하여 저울에 매달아 균형을 확인한 뒤, 물이 담긴 용기에 넣었다. 공기 중에서는 지레의 원리에 의해 저울이 균형을 유지한다. 지레의 원리는 수중에서도 변하지 않으므로, 금괴와 왕관의 부피, 즉 밀도가 같다면 물속에서도 저울의 균형은 유지되어야 한다.

그러나 실제로는 수중에서 균형이 무너졌기 때문에 왕관과 금괴의 밀도가 다르다는 것이 판명되었고, 금세공인의 부정행위가 드러났다.^[16]

2. 2. 유레카 일화의 진실성 (보수적 관점에서의 비판)

"유레카"라는 외침으로 유명한 아르키메데스의 일화는, 왕관이 순금인지 확인하는 과정에서 부력의 원리를 발견했다는 이야기로 널리 알려져 있다. 그러나 이 이야기의 진실성에 대해서는 의문이 제기되기도 한다.

시라쿠사의 참주 히에론 2세는 금세공인에게 순금 왕관 제작을 맡겼으나, 금세공인이 금의 일부를 빼돌렸다는 소문이 돌았다. 히에론 2세는 아르키메데스에게 왕관을 손상시키지 않고 진위 여부를 가려낼 것을 명했다. 아르키메데스는 목욕 중 물이 넘치는 것을 보고 부력의 원리를 깨달았고, "유레카(ΕΥΡΗΚΑ|Eureka^el, 유레카)"(알았다!)를 외치며 알몸으로 뛰쳐나갔다고 전해진다.^[15]

아르키메데스는 왕관과 같은 무게의 순금 덩어리를 준비하여 저울 양쪽에 매달아 균형을 맞춘 후, 물속에 담갔다. 만약 왕관과 금괴의 밀도가 같다면 물속에서도 균형이 유지되어야 하지만, 실제로는 균형이 깨졌다. 이는 왕관에 불순물이 섞여 밀도가 낮아졌기 때문이다.^[16]

하지만, 당시 기술 수준으로 미세한 밀도 차이를 정확하게 측정하는 것은 어려웠을 것이라는 비판이 있다. 또한, 알몸으로 뛰쳐나갔다는 이야기는 과장되었을 가능성이 있다는 지적도 있다.

3. 아르키메데스 원리의 공식과 설명

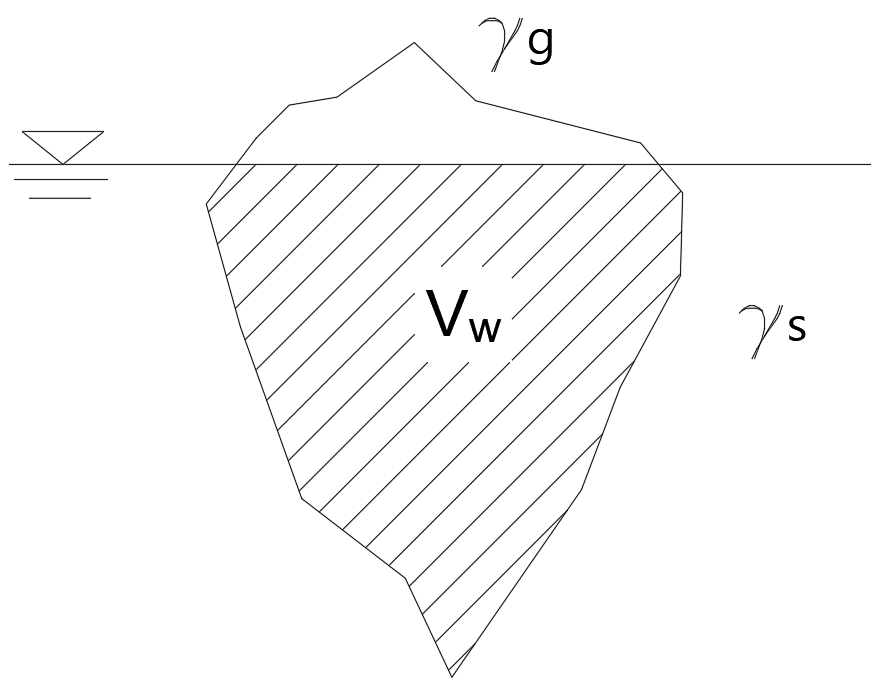
아르키메데스의 원리에 따르면, 물체에 작용하는 부력의 크기는 물체에 잠긴 부분의 부피에 액체의 단위중량을 곱한 값과 같다. 예를 들어 바다에 떠 있는 빙산이 받는 부력은 수중에 있는 빙산의 부피(

V_w

)와 해수의 단위 중량(

\gamma_s = 1.025 t/m^3

)을 곱하여 구할 수 있다.

:

B = \gamma_s V_w

부체의 평형에 관하여에서 아르키메데스는 (기원전 246년경) 다음과 같이 제안했다.

물체에 작용하는 아래 방향의 힘은 물체의 무게이고, 위 방향으로 작용하는 힘은 부력이다. 이 순 힘이 양수이면 물체는 떠오르고, 음수이면 가라앉으며, 0이면 중성 부력을 받아 제자리에 머물러 있는다. 밀어낸 유체의 무게는 밀어낸 유체의 부피에 정비례한다(주변 유체의 밀도가 균일한 경우).

예를 들어, 움직이는 차 안의 헬륨 풍선은 속도를 높이거나 커브를 돌 때, 공기는 차의 가속도와 반대 방향으로 움직이지만 부력 때문에 풍선은 공기에 의해 "밀려나" 차의 가속도와 같은 방향으로 움직인다.

물체가 액체에 잠기면 액체는 밀어낸 액체의 무게에 비례하는 부력이라고 하는 위쪽으로의 힘을 가한다. 따라서 물체에 작용하는 합력은 물체의 무게('아래' 방향의 힘)와 밀어낸 액체의 무게('위' 방향의 힘)의 차이와 같다. 이 두 무게(및 힘)가 같을 때 평형 또는 중성 부력이 달성된다.

아르키메데스가 발견한 원리는 부력의 원리이지만, 왕관 에피소드를 통해 물질에 따른 밀도의 차이를 설명할 때 자주 언급된다. 아르키메데스와 그 후의 학자들은 이 법칙이 자연 과학적인 법칙이라는 것을 깨닫지 못하고, 수학적인 원리라고 생각했다.

3. 1. 부력의 공식

아르키메데스 원리를 사용하면 유체에 부분적으로 또는 완전히 잠긴 모든 부유 물체의 부력을 계산할 수 있다. 부력(F_b^영어)은 유체의 밀도(ρ)에 잠긴 부피(V)와 지구 중력(g)을 곱한 값과 같다.^[1]^[3]

:F_a^영어 = ρgV

여기서 F_a^영어는 잠긴 물체에 작용하는 부력을, ρ는 유체의 밀도, V는 밀어낸 유체의 부피, g는 지구 중력에 의한 가속도를 나타낸다.

따라서 질량이 같은 완전히 잠긴 물체 중에서 부피가 큰 물체가 부력이 더 크다.

3. 2. 겉보기 무게

물체가 유체 속에서 받는 겉보기 무게는 실제 무게에서 부력을 뺀 값과 같다. 예를 들어, 바위에 끈을 매달아 진공 상태에서 무게를 측정했을 때 10 뉴턴이고, 이 바위를 물속에 넣었을 때 3 뉴턴의 무게를 가진 물을 밀어낸다면, 바위가 매달린 끈에 가하는 힘은 10 뉴턴에서 부력 3 뉴턴을 뺀 7 뉴턴이 된다.^[1]^[3] 부력은 바닥까지 완전히 가라앉은 물체의 겉보기 무게를 줄여주기 때문에, 물속에서 물체를 들어 올리는 것이 물 밖으로 꺼내는 것보다 일반적으로 더 쉽다.

완전히 잠긴 물체의 경우, 아르키메데스 원리는 다음과 같이 표현할 수 있다.

: 겉보기 잠김 무게 = 물체의 무게 - 밀어낸 유체의 무게

3. 3. 밀도 측정

아르키메데스의 원리를 이용하면 물체의 밀도를 쉽게 계산할 수 있다. 유체의 밀도에 대한 잠긴 물체의 밀도는 부피를 측정하지 않고도 쉽게 계산할 수 있는데, 다음 공식을 이용한다.

:

\frac { \text {물체의 밀도}} { \text{유체의 밀도} } = \frac { \text{무게}} { \text{무게} - \text{겉보기 잠김 무게}}.\,

^[1]

(이 공식은 예를 들어 밀도계와 수압 평형의 측정 원리를 설명하는 데 사용된다.)

예를 들어, 나무를 물에 떨어뜨리면 부력에 의해 물에 뜨게 된다.

이 법칙의 발견과 관련된 일화는 다음과 같다.

시라쿠사의 참주 히에론 2세는 금세공인에게 금으로 된 왕관을 만들게 했다. 그런데 금세공인이 금의 일부를 훔쳤다는 소문이 돌았고, 히에론은 아르키메데스에게 왕관을 훼손하지 않고 조사하라고 명령했다. 아르키메데스는 목욕을 하다가 물이 넘치는 것을 보고 아르키메데스의 원리의 단서를 발견했다.

아르키메데스는 "유레카(ΕΥΡΗΚΑ|Eureka^el)"(알았다!)라고 외치며 알몸으로 뛰쳐나갔다고 한다.^[15]

아르키메데스는 왕관과 같은 질량의 금괴를 준비하여 물이 담긴 용기에 넣었다. 공기 중에서는 저울은 지레의 원리에 의해 균형이 유지되지만, 수중에서는 균형이 무너졌다. 이는 왕관과 금괴의 밀도가 다르다는 것을 의미하며, 금세공인의 부정 행위가 드러났다.^[16] 금세공인은 사형에 처해졌다고 전해진다.

유럽의 학교에서는 아르키메데스의 원리에 따라 물체의 부피를 측정하는 실험을 할 때 Eureka can(displacement can, 유레카 캔)이라는 기구를 사용한다.

4. 힘과 평형

유체에 잠긴 직육면체를 생각해 보자. 윗면과 아랫면은 중력 방향에 수직이다. 유체는 각 면에 법선력을 가하지만, 부력에 기여하는 법선력은 윗면과 아랫면에 작용하는 법선력뿐이다.^[1] 아랫면과 윗면 사이의 압력 차이는 높이(잠김 깊이의 차이)에 정비례한다. 압력 차이에 면적을 곱하면 직육면체에 작용하는 순 힘, 즉 부력이 발생하며, 이는 직육면체가 밀어낸 유체의 무게와 크기가 같다.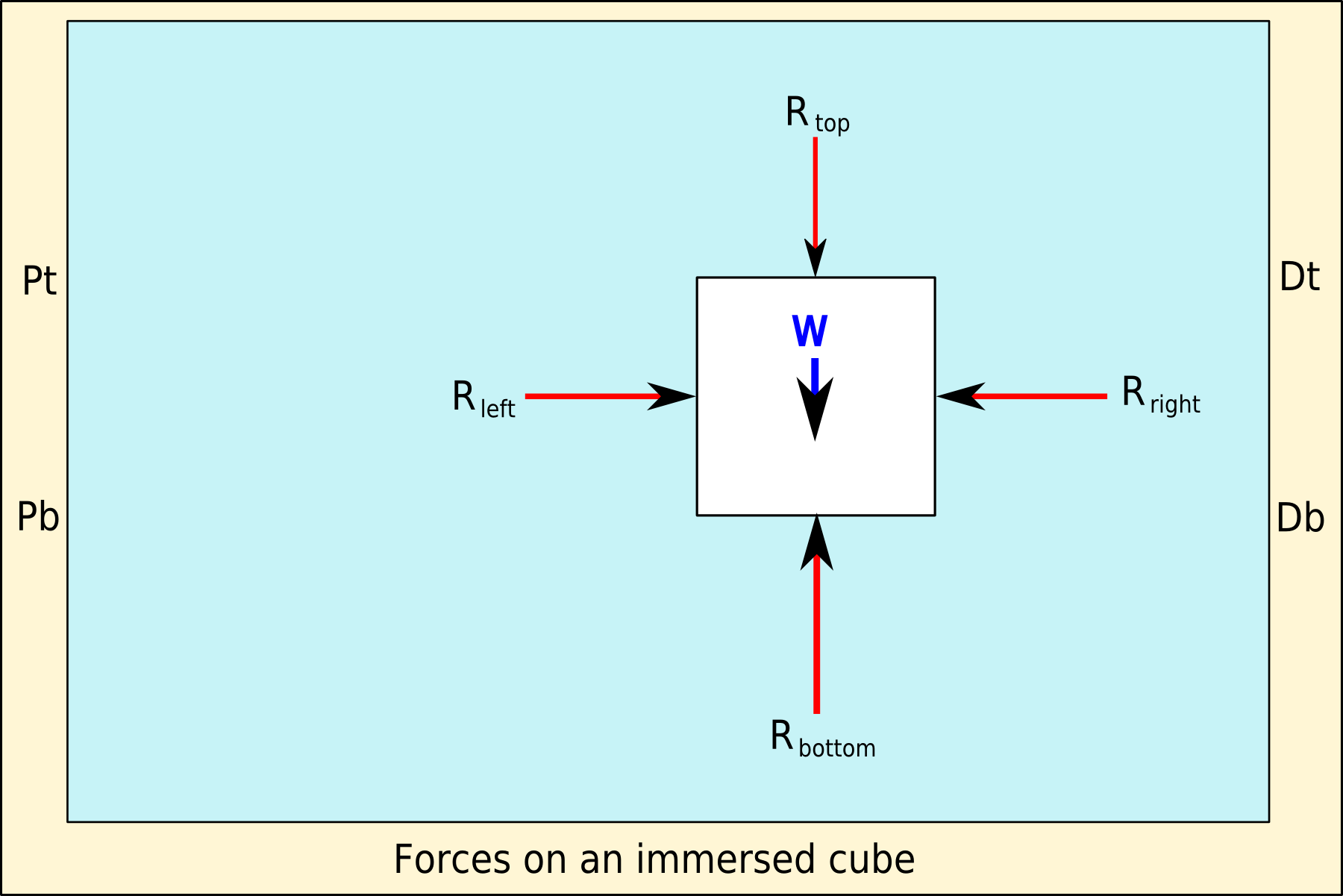

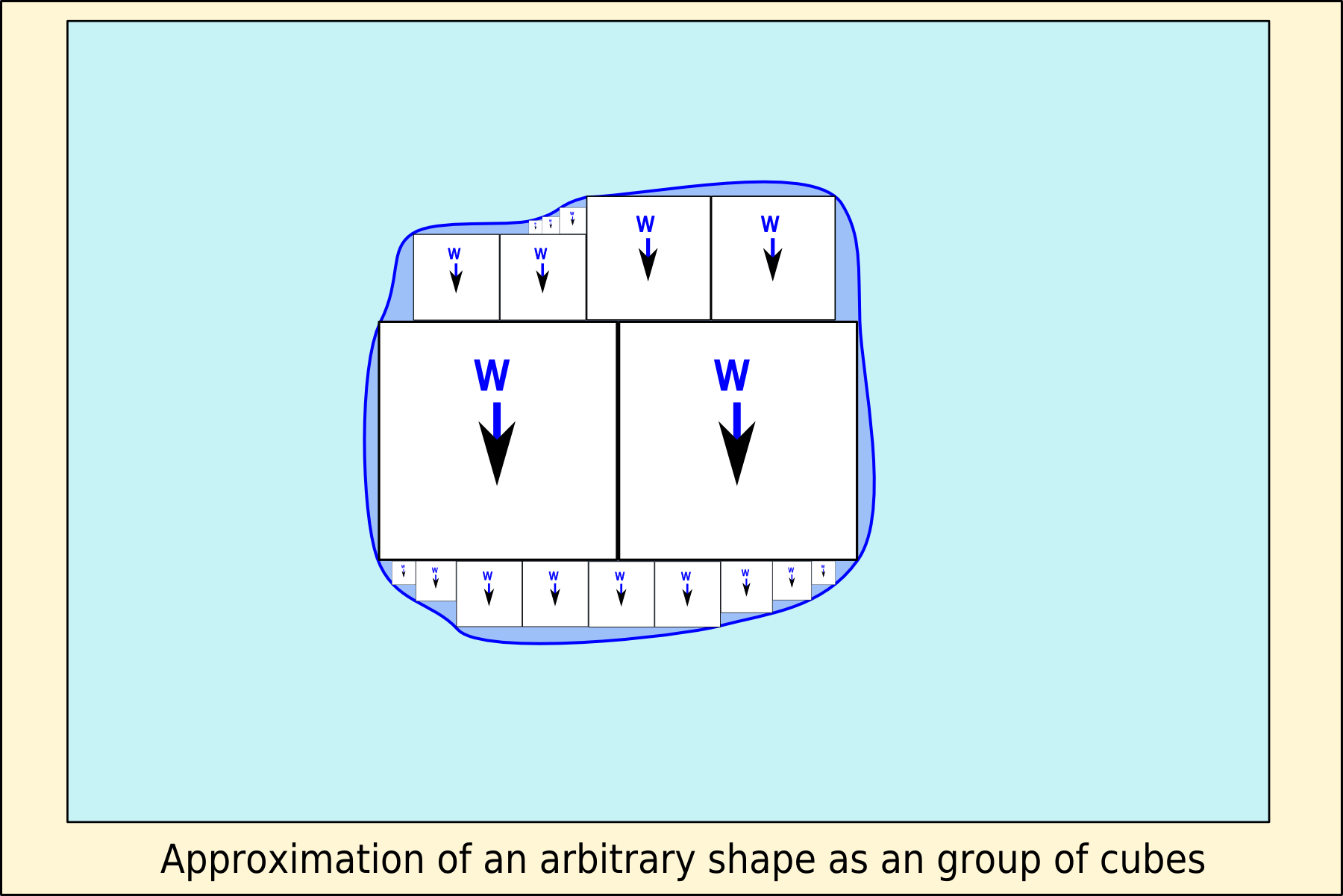
밀어낸 유체의 무게는 밀어낸 유체의 부피에 정비례한다(주변 유체의 밀도가 균일한 경우). 유체 속에 있는 물체의 무게는 물체에 작용하는 힘 때문에 감소하는데, 이를 부력이라고 한다. 물체에 작용하는 부력(F_b)은 물체가 밀어낸 유체의 무게, 즉 유체의 밀도(ρ)에 잠긴 부피(V)와 지구 중력(g)을 곱한 값과 같다.^[1]^[3]

이 관계는 다음 식으로 나타낼 수 있다.

:

F_{a} = \rho g V

여기서

F_{a}

는 잠긴 물체에 작용하는 부력을 나타내고,

\rho

는 유체의 밀도,

V

는 밀어낸 유체의 부피,

g

는 지구 중력에 의한 가속도를 나타낸다.

물체가 액체에 잠기면 액체는 밀어낸 액체의 무게에 비례하는 부력이라고 하는 위쪽으로의 힘을 가한다. 따라서 물체에 작용하는 합력은 물체의 무게('아래' 방향의 힘)와 밀어낸 액체의 무게('위' 방향의 힘)의 차이와 같다. 이 두 무게(및 힘)가 같을 때 평형 또는 중성 부력이 달성된다.

평형 상태의 유체 내부 압력을 계산하는 방정식은 다음과 같다.

:

\mathbf{f}+\operatorname{div}\,\sigma=0

여기서 '''f'''는 유체에 대한 외부 장에 의해 가해지는 힘 밀도이고, ''σ''는 코시 응력 텐서이다. 이 경우 응력 텐서는 항등 텐서에 비례한다.

:

\sigma_{ij}=-p\delta_{ij}.\,

여기서 ''δ_ij''는 크로네커 델타이다. 이를 사용하여 위의 방정식은 다음과 같다.

:

\mathbf{f}=\nabla p.\,

외부 힘장이 보존적이라고 가정하면, 즉 어떤 스칼라 값을 갖는 함수의 음의 기울기로 쓸 수 있다.

:

\mathbf{f}=-\nabla\Phi.\,

그렇다면 다음과 같다.

:

\nabla(p+\Phi)=0 \Longrightarrow p+\Phi = \text{constant}.\,

따라서 유체의 열린 표면의 모양은 적용된 외부 보존력장의 등전위 평면과 같다. ''z''축이 아래쪽을 가리키도록 한다. 이 경우 필드는 중력이므로 Φ = −''ρ_fgz''이며 여기서 ''g''는 중력 가속도이고, ''ρ_f''는 유체의 질량 밀도이다. 표면에서 압력을 0으로 취하면, 여기서 ''z''는 0이므로, 상수는 0이 되고, 따라서 중력에 영향을 받는 유체 내부의 압력은

:

p=\rho_f g z.\,

따라서 압력은 액체의 표면 아래 깊이와 함께 증가하며, 여기서 ''z''는 액체의 표면에서 내부까지의 거리를 나타낸다. 수직 깊이가 0이 아닌 모든 물체는 상단과 하단에 서로 다른 압력을 받으며, 하단의 압력이 더 크다. 이러한 압력의 차이는 부력의 힘을 발생시킨다.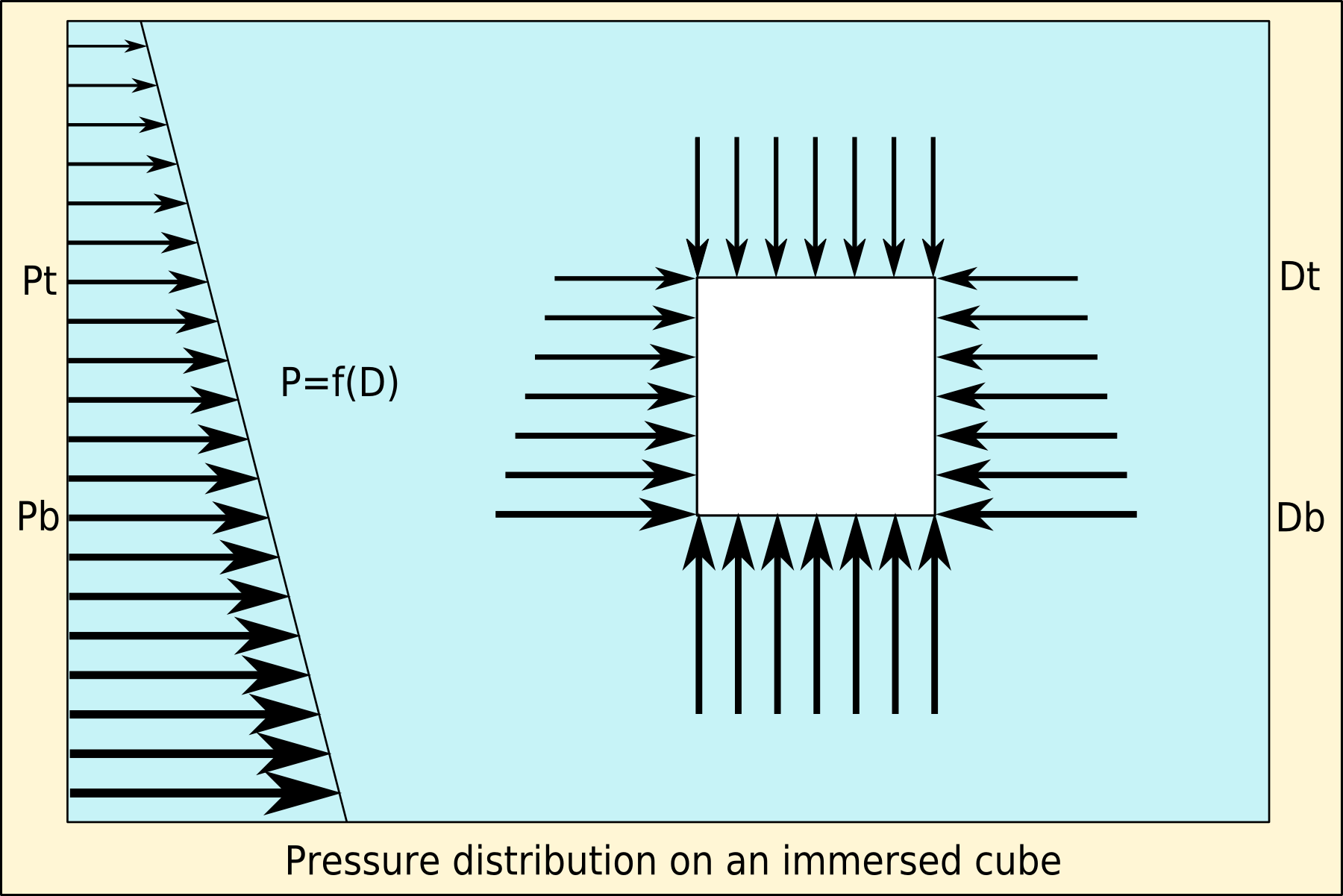

5. 부력의 활용

아르키메데스의 원리는 여러 분야에서 활용된다. 빙산의 경우, 아르키메데스의 원리에 따라 빙산에 작용하는 부력의 크기는 빙산의 잠긴 부분의 부피에 해수의 단위중량을 곱한 값과 같다. 해수의 단위중량이 $\gamma_s = 1.025 t/m^3$ 일 때, 수중에 있는 빙산의 부피를 V_w라 하면 부력(B)은 다음과 같이 계산할 수 있다.

$B = \gamma_s V_w$

5. 1. 선박 설계

배가 물에 뜨는 원리는 아르키메데스의 원리로 설명된다. 아르키메데스의 논문 ''부체에 관하여''의 명제 5는 다음과 같이 말한다.^[7]

즉, 배는 자체 무게와 같은 무게의 물을 밀어냄으로써 부력을 얻는다. 1톤의 고체 철 블록은 물보다 거의 8배 더 밀도가 높기 때문에 잠길 때 1/8톤의 물만 밀어내는데, 이는 물에 뜨기에 충분하지 않다. 그러나 같은 철 블록을 그릇 모양으로 만들면, 무게는 여전히 1톤이지만, 물에 넣으면 블록일 때보다 더 많은 양의 물을 밀어낸다. 철 그릇을 더 깊이 잠글수록 더 많은 물을 밀어내고, 그에 따라 부력도 커진다. 부력이 1톤과 같아지면 더 이상 가라앉지 않는다.

어떤 배든 자체 무게와 같은 무게의 물을 밀어내면 뜬다. 이것은 "부력의 원리"라고도 불린다. 모든 배는 자체 무게와 최소한 같은 무게의 물을 밀어내도록 설계되어야 한다. 10,000톤의 선체는 10,000톤의 물을 밀어내고 가라앉는 것을 방지하기 위해 물 위에 약간의 선체를 유지할 수 있도록 충분히 넓고, 길고, 깊게 만들어야 한다.

5. 2. 잠수함 및 비행선

잠수함과 비행선은 각각 물과 공기 중에서 작동하지만, 둘 다 아르키메데스의 원리를 이용하여 부력을 조절한다. 시라쿠사의 아르키메데스는 부체에 관하여 명제 5에서 "어떤 부유 물체든 자기 자신의 무게와 같은 유체를 밀어낸다."라고 하였다.^[7]

잠수함은 물속에 잠겨 있으므로 밀어낸 물의 무게가 잠수함의 무게와 같다. 철은 물보다 밀도가 প্রায় 8배 높아 철 블록은 가라앉지만, 같은 무게의 철이라도 그릇 모양으로 만들면 더 많은 물을 밀어낼 수 있어 부력이 커지고 물에 뜰 수 있다.

비행선도 마찬가지로, 무게가 100톤인 비행선은 100톤의 공기를 밀어내야 한다. 밀어내는 공기의 양을 조절하여 상승, 하강하거나 일정한 고도에서 비행할 수 있다.

배, 잠수함, 비행선 모두 자체 무게와 최소한 같은 무게의 유체를 밀어내도록 설계되어야 한다. 예를 들어 10,000톤의 선체는 10,000톤의 물을 밀어낼 수 있도록 충분히 커야 한다.^[7]

5. 3. 유레카 캔 (Eureka can)

유럽의 학교에서는 아르키메데스의 원리에 따라 물체의 부피를 측정하는 실험을 할 때 유레카 캔(Eureka can, displacement can)이라는 기구를 자주 사용한다. 이 기구는 측면 상부에 비스듬히 아래로 향한 배수관이 하나 달려 있다. 배수관 위치 이상으로 물을 채워 넘쳐흐르는 것을 기다린 다음 배수관 아래에 눈금 실린더를 설치하여 배수량을 측정한다.^[15]

참조

_[1] 웹사이트 What is buoyant force? https://www.khanacad[...]
_[2] 논문 The diving "Law-ers": A brief resume of their lives. http://archive.rubic[...] 2009-06-13
_[3] 웹사이트 The buoyant force http://physics.bu.ed[...] 2023-09-03
_[4] 웹사이트 Floater clustering in a standing wave: Capillarity effects drive hydrophilic or hydrophobic particles to congregate at specific points on a wave http://www.weizmann.[...] 2005-06-23
_[5] 간행물 Archimedes's principle gets updated
_[6] 논문 Using surface integrals for checking the Archimedes' law of buoyancy
_[7] 웹사이트 The works of Archimedes https://archive.org/[...] Cambridge, University Press 2010-03-11
_[8] 서적 Basic Principles of Physics https://books.google[...] Pitambar Publishing 1997
_[9] 서적 Research on Physics Education https://books.google[...] IOS Press 2004
_[10] 웹사이트 Proof of Concept http://www.carpeastr[...]
_[11] 웹사이트 The Golden Crown https://physics.webe[...]
_[12] 웹사이트 'Eureka!' – The Story of Archimedes and the Golden Crown http://www.longlongt[...] 2014-05-16
_[13] 문서 空気中に出ている部分の浮力を無視していることに注意。
_[14] 문서 氷の方が密度が小さく、温度によっても異なるが''ρ''_氷 = 920 kg/m³、水は ''ρ''_水 = 1000 kg/m³ 程度であり、かなりの差があることが分かっている。
_[15] 문서 もっとも、当時の古代ギリシアでは人間は裸で運動するのが普通で、裸で外を走ったり公衆の面前で裸になったりしても特段に珍しいことではなかった。
_[16] 웹사이트 The Golden Crown (Introduction) http://www.math.nyu.[...] New York University 2012-04-12

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com